Introduction of Diameter and Radius
Diameter: Diameter is a mathematical measurement, defined as the straight-line section that runs along the middle of any sphere or circle and connects any two points on its circumference. Simply stated, its diameter could be seen as its length – typically expressed in centimeters, inches, or meters.
Radius: Radius Radii are geometric dimensions associated with circles and spheres. A radius measures the distance that extends from any point on a circle or sphere’s central point to any other location on it, as well as from its center out to all edges; its value equals half the diameter’s width – this value can also be expressed using centimeters, inches or meters units of measure.
Diameter refers to the length of a circle or sphere while radius measures how far from center to edge it is; diameter equals twice its size of radius measurement. Both these measurements play an essential part in geometry that can also be utilized in other disciplines like physics, mathematics engineering, and daily life.
What is Diameter?
Diameter is an elementary geometric measure, used to refer to the straight-line segment that runs along the centerline of any sphere or circle, connecting any two points along its circumference. Simply stated, its width or diameter could also be considered its length or circumference.
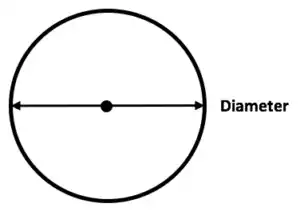
Diameter is one of the key characteristics of spheres and circles and is typically denoted with “D.” Measured in centimeters, inches, or meters, its length provides information on the dimensions of either an object sphere, or circle.
To calculate the radius of a circle. the formula is;
Diameter (D) = 2 x radius (r)
Formula (1) indicates the diameter (r) as being equivalent to the radius from its center to a point on its circumference, when multiplied by two this creates the diameter. Their relationship remains constant across all circles.
Understanding diameter is fundamental for numerous practical and mathematical uses, and is directly connected with its companion formula:
Circumference (C) = px Diameter (D)
“p” refers to the mathematical constant Pi, approximately 3.14159. Pi can also be defined as the measurement between the outer and inner edges of a circle and can serve as a multiplier of its circumference.
Understanding diameter can be useful when measuring circular objects plates, wheels pipes, and wheels – as well as being employed in areas like architecture engineering and geometry for designing construction purposes and calculations purposes.
What is Radius?
The radius is an integral geometric measurement associated with circles and spheres. It measures the distance that extends from any point within any sphere or circle to its circumference point – in other words, connecting its center point with its edge via straight line segments.
The radius, often represented with an “r”, can be measured in centimeters or inches and serves as a fundamental property of both spheres and circles – making its existence essential for many mathematical calculations and equations.
A circle’s radius equals half its diameter; thus its relationship can be described using this equation:
Radius (r) = Diameter (D) / 2.
Divide the diameter by two, and you will obtain its radius; this calculation applies to any sphere or circle.
Acknowledging the radius is essential since its value directly ties into both the circumference and diameter of a circle. By knowing its radius and applying an equation such as this one to it, one may determine the circumference of any circle.
Circumference (C) = 2p + Radius (r).
The letter “p” symbolizes the mathematical constant pi, which equals approximately 3.14159. Circumference (or circumference) refers to the distance to outside a circle and can be obtained by dividing 2p by the radius.
The area of a circle may be calculated using its radius using this formula:
Area (A) = P x Radius (r).
The area is the area that surrounds a circle, determined by multiplying its square.
The radius can be used across many disciplines and fields – engineering, mathematics, physics as well as everyday life – from engineering and mathematics to physics and everyday use. It provides dimensions, sizes, and proportions of circular objects, satellite orbit calculations, planet measurements as well as design for architecture projects where circles or spheres are often employed.
What are the significances of Diameter?
Diameters are briefly covered during Key Stage Two math classes; however, in maths courses at Key Stage Three and higher levels, they are studied more in-depth. The aim is to teach students about formulae for calculating circumference and area calculations of circles as well as demonstrate how diameters can assist in solving issues.
Real life contains numerous circles; knowing their circumference and size can help us better comprehend how they should be utilized.
Dials that can be found in real life.
Tires on a Car
Tire sizes vary considerably and when purchasing new tires for our vehicles it is essential that we select the appropriate tire size based on wheel diameter to avoid costly errors in tire selection.
Take for instance tire size P225/65R17 to demonstrate this point: its number indicates both width and aspect ratio as well as the wheel size intended. 18 typically appears on its sidewalls to indicate it can only fit wheels that measure 15 inches or greater otherwise this tire won’t work.
Why is Radius Important?
- Measurement and Size: Size and Measurement Dimensiuni The radius is a measure that connects the center of a sphere or circle to its edge, helping determine both size and proportions in circular items. Furthermore, it serves as a basis for various applications of measurement.
- Circumference Calculation: Radius and Circumference are inextricably linked, making its knowledge an accurate measure of distance around an outer edge shape by means of C = 2pr where C denotes Circumference and P denotes Pi – the mathematical constant.
- Area Calculation: Calculating Area Dimensiuni is crucial when it comes to calculating the surface area of a circle, with formula A = pr2 linking its radius directly with its circumference area.
- Mathematics: Diameter relationships in mathematics demonstrate how it’s related to other geometric properties, for instance, the diameter is double its predecessor and their connections between diameter, radius, and circumference remain consistent across circles.
- Practical Applications: Practical Applications The radius can be applied across many disciplines, from engineering and architecture to physics and geometry. Its use assists with distance determination, taking accurate measurements, designing structures with circular forms, and solving any related issues.
Differences of Diameter and Radius
Diameter and radius are fundamental terms in geometry, particularly when dealing with circles and circular shapes. While they both relate to measurements within circles, they serve distinct purposes and have different characteristics.
Let’s explore the differences between diameter and radius:
- Definition:
- Diameter: A circle’s diameter consists of straight line segments running along its center to connect two points around its circumference; more simply put, this length across the broadest part of its circumference is known as its diameter.
- Radius: A circle’s radius can be defined as the total length of straight lines running beyond its center to any point along its circumference, measuring distance from center to edge of its circle.
- Mathematical Representation:
- Diameter: It is commonly represented by the symbol “d.”
- Radius: It is often symbolized by the letter “r.”
- Calculation:
- Diameter: The diameter is calculated by doubling the length of the radius: Diameter = 2 × Radius.
- Radius: The radius is calculated by halving the length of the diameter: Radius = Diameter ÷ 2.
- Relationship:
- The diameter and radius are related by a simple equation: Diameter = 2 × Radius. This relationship highlights the connection between the two measurements.
- Measurement Length:
- Diameter: The diameter is a longer measurement, as it spans across the entire circle.
- Radius: The radius is a shorter measurement, extending only from the center to the edge.
- Application:
- Diameter: It is crucial for calculations involving the circumference, area, and properties of circles. It’s also used in various real-world scenarios, such as measuring the width of circular objects.
- Radius: The radius is essential for understanding circular shapes and their properties. It plays a significant role in calculating the length of arcs, as well as in engineering and design.
- Importance:
- Diameter: It’s important for determining the size and dimensions of circular objects and plays a role in numerous mathematical and practical contexts.
- Radius: The radius provides insight into the center-to-edge distance of circular objects and influences their overall structure and design.
- Visual Representation:
- Diameter: Imagine a line segment passing through the center of a circle, spanning from one side to the other.
- Radius: Envision a line extending from the center of the circle to a point on its edge.
Diameter and Radius are interconnected yet distinct concepts that contribute to our understanding of circles and their properties. While the diameter measures the widest part of a circle, the radius gauges the distance from the center to any point on the circle’s boundary. Both measurements play vital roles in mathematics, geometry, engineering, and everyday applications.
Conclusion
The concepts of Diameter and Radius form the building blocks of understanding circles and various geometric shapes. Their significance spans across mathematics, science, engineering, and everyday life. By comprehending the relationship between these measurements, we unlock insights into the world around us, from the tiniest particles to the grandest structures.